Riyazi funksiyaların qurulması bugünki, elektron dərsimizin əsas mövzusu olacaq. Odur ki, əziz dostlar, dəyərli oxucularım və dinləyicilərim, həmçinin gadirov.com saytının daimi ziyarətçiləri, youtube abunəçilərim və sosial şəbəkə istifadəçilərim sizləri Hesablama Əməliyyatları moduluna həsr olunmuş elektron dərslikdə salamlayıram. Bildirmək istəyirəm ki, bu nəşrin məzmunu müstəsna olaraq “Azərbaycanda Peşə Təhsili və Təliminin inkişafına Avropa İttifaqının dəstəyi” Texniki Yardım layihəsinin məsuliyyətidir və heç bir halda Avropa İttifaqının mövqeyini əks etdirmir. Qeyd etmək istəyirəm ki, bu saytda dərc olunacaq Hesablama Əməliyyatları modulu ilə bağlı mövzular Hesablama Əməliyyatları kitabının elektron versiyasında da mövcuddur. Həmin dərslikdən də istifadə edə bilərsiniz.
Məqalənin mündəricatı
Riyazi funksiyaların qurulması
Funksiya nədir?
Riyaziyyatın əsas anlayışlarından biri “funksiya”dır. Funksiya sabit və ya dəyişən kəmiyyətlərdən istifadə edilərək verilə bilər. Dəyişən kəmiyyət müxtəlif ədədi qiymət ala bilən kəmiyyətə, sabit kəmiyyət isə yalnız bir ədədi qiymət ala bilən kəmiyyətə deyilir. Məsələn, küləyin sürəti, avtomobilin hərəkəti, qrunt suyunun təzyiqi və s. dəyişən kəmiyyətlərdir. İlin fəsillərinin sayı, çevrənin uzunluğunun diametrinə olan nisbəti və s. sabit kəmiyyətdir.
Funksiya hər hansı kəmiyyətin bir qiyməti digər kəmiyyətin də müəyyən qayda ilə ona uyğun hər hansı qiymət almasına səbəb olur. Onda ikinci dəyişən kəmiyyət birincidən asılı olur. Birinci dəyişənə sərbəst (asılı olmayan), ikinci dəyişənə isə asılı dəyişən deyilir. Sərbəst dəyişənə arqument, asılı dəyişənə isə onun funksiyası deyilir. X çoxluğundan hər bir x elementinə Y çoxluğunun yeganə y elementini qarşı qoyan uyğunluğa (qaydaya) funksiya deyilir və y = f (x) kimi yazılır, y-ə x-in obrazı deyilir.
Funksiyanın təyin oblastı, arqumentin ala biləcəyi qiymətlər çoxluğuna deyilir. Arqumentdən asılı olaraq, funksiyanın aldığı qiymətlər çoxluğuna isə onun qiymətlər çoxluğu deyilir.
Funksiya ümumi şəkildə y=f(x) kimi işarə olunur. Burada x – arqument, f(x) isə funksiyadır.
Funksiyanın analitik üsulla (düsturla) verilməsi
Funksiya analitik üsulla (düsturla) verilə bilər.
Məsələn, y(x) = x2 + 1 və ya y = x2 + 1
x = 3 olduqda, y(3) = 32 + 1= 10 olur. y = 2 olduqda x = 1 və ya x = – 1 olar.
Funksiyanın cədvəl şəklində verilməsi
Funksiya cədvəl şəklində verilə bilər. Məsələn:
Cədvələ əsasən deyə bilərik ki, x = – 3 olduqda, y = 2 olur. x = 1 olduqda, y = 2 olur. Bu cədvəl x-in – 3; – 1; 0; 1; 2; 3 tam qiymətləri üçün hər hansı funksiyanın qiymətlər cədvəlidir.
Funksiyanın qrafik şəklində verilməsi
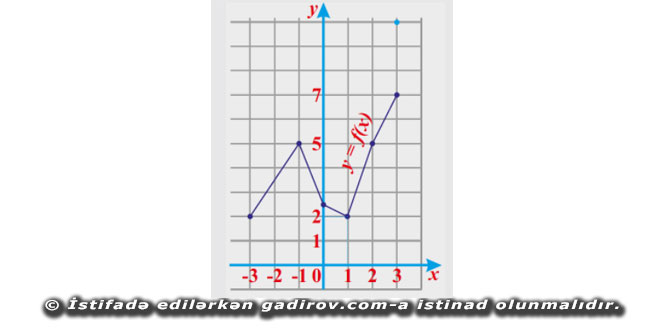
Funksiya qrafik şəklində verilə bilər. Funksional asılılığı əyani şəkildə təsvir etmək üçün qrafikdən istifadə edilir. Yuxarıdakı cədvəldə verilmiş koordinatlar cütünü koordinat sistemində qeyd edin və onları ardıcıl olaraq xətlə birləşdirin. Qrafikə əsasən, məsələn, x = 1 olduqda, y = 2 qiymətini aldığını demək olar.
© İstifadə edilərkən gadirov.com-a istinad olunmalıdır
